LISTAS ENLAZADAS
· Vector dinámico
· La lista enlazada
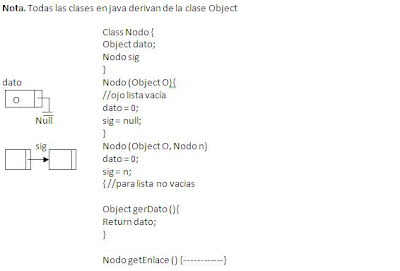
Es una E.D Dinámica formada por un conjunto de Nodo conectado a través de 1 enlace (sig), queda definida basicamente x. .
Nombre, 1 enlace al 1er Nodo (Elemento) y enlace al último (Elemento)
· Operaciones caso base
- Insertar . Lista vacía
- Eliminar . 1 solo elemento en la lista
- Buscar . +1 elemento en la lista
- Ordenar
- Operaciones
- Constructor
- Lista Vacia
Operaciones lista enlazadas
- Ins Posterior
Contar Nodo de una lista
Public int CantNodo
Nodo = pri, int cant = 0;
While (Actual (= null)){
Cant++;
Actual = Actual.sig; // Avanzamos
}
}
public void InsPos_n (Object Obj, int pos){
if (ListaVacia ()) InsertarFrente();
else {
If (pos == 1){InsetarFrente();}
If (pos == cantElem ()){InsertarPosterior;}
Else {
NodoActual = pri;
For (int i=0; i<pos-1; i++){
Actual = Actual.sig;
NodoNuevo = new Nodo (Obj, Actual.sig)
}
}
}
Listas enlazadas
// Hasta aquí
Public class ListaSimple {
Prívate Nodo pri;
Prívate Nodo ult;
Prívate String nombre;
}
Public ListaSimple {
Pri = ult = null;
Nombre = “” ;
}
Public ListaSimple (){
Pri = ult = null;
Nombre = n;
}
Public boolean ListaVacia (){
Return pri == null;
}
Public void InsFrente (Object Ob){-----------}
Public void InsPosterior (Object Ob){-----------}
Public void InsPosicion (Object Ob, int pos){-----------}
ALGORITMO
Public Object DelPos_n (){
If (Elem =1){
Obejct DatoARemover = pos.dato;
If pri.Equals (pos)
Pri.ult = null;
Else {
Nodo Actual
Public Object DelPos_n (int Pos){
If (ListaVacia) return Error;
If (pos == 1) DelFrente ();
If (pos == NroElem) DelPosterior ();
Object DatoARemover;
Else {
If (pri.Equals (ult)) {
Pri = ult = null;
Return DatoARemover;
}
Else {
Nodo Actual = pri;
For (int i=0; i<pos; i++)
Actual = Actual.sig;
Nodo ABorrar = Actual.sig;
DatoARemover = (Actual.sig).dato; ó
(Aborrar.dato);
Actual.sig = (Actual.sig).sig; ó
ABorrar.sig;
ABorrar.sig = null;
Return DatoARemover;
Public void Update Frente (object Obj Nuevo){
If (ListaVacia ()) System.out.PrintLn (“Error”);
Else {
Pri.dato = ObjNuevo;
Public void Update Pos (Object Ob){
If (ListaVacia ()) JOptionPane.ShowMessageDialog (“Error”);
Else {
Ult.dato = Ob;
}
Public void Update Pos_n (Object ObjNuevo, int pos){
If (ListaVacia ()) System.out.PrinLn (“Erro”);
If (pos ==1) UpdateFrente (ObjNuevo)
If (pos == NroElem) UpdatePost (Obj Nuevo);
Else {
NodoActual = pri;
For (int i=1; i ≤ pos; i++){
Actual = Actual .sig;
Actual.dato = ObjNuevo;
}
}
Public void Mostrar Lista (){
Nodo Actual = pri;
While (Actual ¡= null){
JoptionPane.ShowMessageDialog (“Error”);
Actual = Actual.sig;
}
}
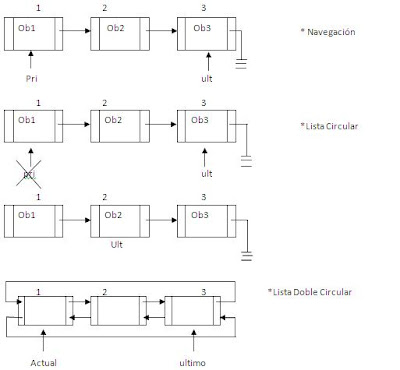
LISTAS CIRCULARES
EJEMPLOS DE RECORRIDOS
Class NodoDoble{
Objec Dato;
Nodo sig;
Nodoant;
Public NodoDato(){--}
}
Class ListaDobleCircular{
Stirng nombre;
Nodo ultimo;
Nodo Actual; // Opcional
}
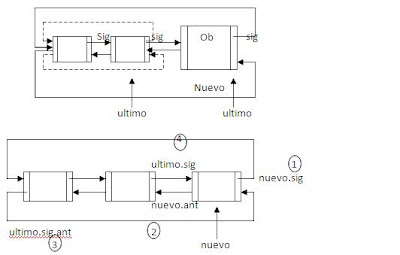
INSERCIONES
Nuevo.sig=ultimo.sig;
Nuevo.ant=ultimo;
Ultimo.sig.ant=Nuevo;
Ultimo.sig=Nuevo;
Ultimo=Nuevo;
Insertar Pos_n
a) Vacia() crear Nodo
b) ̃Vacia()
nuevo.sig = Actual.sig;
nuevo.ant=actual;
actual.sig.ant=Nuevo;
actual=nuevo;
ELIMINACIONES
· Delete ultimo
a) listaVacia() :
JOptionPaneShowmessageDialog(“Error”);
b) ̃listaVacia()
- Delete primero
A) ListaVacia() = JOptionPaneShowmessageDialog(“Error”);
B) ̃ListaVacia
1. Actual.sig.ant = ultimo;
2. Ultimo.sig = Actual.sig;
3. Actual.sig=Actual.ant=null;
Delete Pos_n
a) Vacia() = JOptionPaneShowmessageDialog(“Error”);
b) ̃Vacia()
Au.sig = Actual.sig;
Actual.sig.ant = Aux;
Actual.sig = Actual.ant = null;
ARBOLES
Es una ED no lineal que consta de un conjunto de nodos y un conjunto de ramas
Un árbol es un conjunto finito de 0 o más nodos v1,v2,...,vn tales que:
1- existe un Nodo el cual se distingue de los demás, al mismo lo vamos llamar raíz
2- los demás elementos del conjuntos quedan particionados en m>=0 conjuntos disjuntos T1,T2,...,TN los cuales son arboles.
Los elementos T1,T2,...,TN son llamados subarboles. Vemos aquí la naturaleza recursiva de la estructura árbol, puesto que definimos árbol en termino de arboles.
- El grado interior del nodo raíz es nulo, esto quiere decir que no
existen ramificaciones de entrada hacia él.
- Los Nodos que tienen grado exterior=0 se dicen que son nodos hojas de un árbol.
- Se dice que un árbol esta en niveles, los cuales están determinados
por la longitud de la trayectoria desde la raíz hacia dicho nodo.
- El peso de un árbol está determinado por el numero de nodos hojas
- La altura de un árbol es 1 mas el mayor nivel de nodos
- Un conjunto de arboles enraizados se dice que forman un bosque.
1- existe un Nodo el cual se distingue de los demás, al mismo lo vamos llamar raíz
2- los demás elementos del conjuntos quedan particionados en m>=0 conjuntos disjuntos T1,T2,...,TN los cuales son arboles.
Los elementos T1,T2,...,TN son llamados subarboles. Vemos aquí la naturaleza recursiva de la estructura árbol, puesto que definimos árbol en termino de arboles.
- El grado interior del nodo raíz es nulo, esto quiere decir que no
existen ramificaciones de entrada hacia él.
- Los Nodos que tienen grado exterior=0 se dicen que son nodos hojas de un árbol.
- Se dice que un árbol esta en niveles, los cuales están determinados
por la longitud de la trayectoria desde la raíz hacia dicho nodo.
- El peso de un árbol está determinado por el numero de nodos hojas
- La altura de un árbol es 1 mas el mayor nivel de nodos
- Un conjunto de arboles enraizados se dice que forman un bosque.
Otras definiciones
· Un árbol es un conjunto finito de nodos
· Un árbol es un conjunto de subárboles
Arboles Binarios
Un árbol binario es un caso especial de arboles generales.
Es un conjunto finito de 0 nodos, o mas que tienen un subconjunto
disjunto de 2 nodos, uno denominado subárbol derecho y otro
subárbol izquierdo.
Es un conjunto finito de 0 nodos, o mas que tienen un subconjunto
disjunto de 2 nodos, uno denominado subárbol derecho y otro
subárbol izquierdo.
Recorrido de un Árbol
Dependiendo del orden de lectura del nodo raíz, se clasifican en:
- PreOrden
- InOrden
- PostOrden
- Pre-Orden (raíz-izq-der)
- In-Orden (izq-raíz-der)
- Post-Orden (izq-der-raíz)
GRAFOS
Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de pares de vértices, llamado arista que pueden ser orientados o no. Típicamente, un grafo se representa mediante una serie de puntos (los vértices) conectados por líneas (las aristas).
Diagrama de Grafo con 6 vertices y 7 aristas